ANALISIS KOMPARATIF : UJI T
ANALISIS KOMPARATIF : UJI T
Link Makalah : https://drive.google.com/file/d/1V1Qmk1war6gVmB7e7INuvHDwaIpNbbwW/view?usp=sharing
Link Video : https://youtu.be/MhuRI0UrXZk?si=DK_eNtLhCX32dQMp
Link Contoh Artikel : https://drive.google.com/file/d/17q0E-pDdEKueN3flhM1j57E36GATSVTu/view?usp=sharing
Link Cek Plagiasi : https://drive.google.com/file/d/1QN9xS121FwHlj6ZjiUPWtsZORrS7po3z/view?usp=sharing
ANALISIS
KOMPARATIF : UJI T ( T TEST )
MAKALAH
Disusun untuk memenuhi tugas mata kuliah Statistika
Inferensial
Dosen pengampu Prof. Dr. Parno, M.Si.
OLEH
IVAN DANAR ADITYA IRAWAN
NIM 230321810991
UNIVERSITAS NEGERI MALANG
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
PROGRAM STUDI MAGISTER PENDIDIKAN FISIKA
OKTOBER 2023
BAB I
UJI T
A.
DEFINISI
Uji t atau yang biasa disebut dengan t-test,
adalah salah satu metode yang
digunakan dalam proses analisis data melalui perbandingan
nilai rerata
dua kelompok sampel penelitian. Uji-t berfungsi untuk membandingkan rata-rata
dua kelompok untuk menentukan ada
tidaknya
perbedaan signifikan antara
dua kelompok tersebut[1]. Uji t merupakan
analalisis statistik parametrik sehingga dalam melakukan pengujian perlu
memperhatikan syarat-syarat dan asumsi tertentu. Secara umum uji t dapat
dilakukan pada tiga situasi, yaitu a). Dua kelompok independen (misalnya membandingkan antara rerata kelas eksperimen dengan kelas kontrol); b) dua kelompok
berpasangan (misalnya membandingkan rerata skor pretest dan posttest dalam satu kelas); dan (c)
kelompok sampel dan populasi (misalnya membandingkan rerata dari suatu sampel dengan rerata populasi). Pengujian dengan t-test
ini diterapkan
guna
mengetahui dua kelompok sampel yang dibandingkan mempunyai perbedaan yang signifikan atau tidak. Pengujian dapat
dilakukan baik secara manual, excel,
dan IBM SPSS[2], [3].
B.
SYARAT
ANALISIS
Pengujian t test dilakukan
melalui perbandingan
nilai antara t
hitung dengan t tabel. Namun, sebelum melakukan pengujian harus memenuhi
beberapa syarat dan uji asumsi diantaranya adalah
1.
Ukuran sampel memadahi
Pengujian statistik
dengan uji t harus memiliki data sampel dengan jumlah besar agar hasil yang
diperoleh menjadi lebih bisa dipertanggungjawabkan. Secara umum syarat minimal
pengujian dengan uji t agar hasil yang diperoleh valid adalah
sekurang-kurangnya adalah 30 sampel. Jika tidak memenuhi jumlah tersebut maka
dapat dilakukan pengujian alternatif dengan uji non parametrik.
2.
Data Interval atau rasio
Data interval dan data
rasio adalah jenis data yang dapat digunakan untuk melakukan pengujian dengan
uji t. Jika tidak menggunakan dua jenis data tersebut maka dapat dilakukan
pengujiand engan uji non parametrik.
3.
Uji Normalitas
Uji normalitas merupakan salah satu uji statistik yang berfungsi
guna
mengetahui apakah data yang
didapatkan suatu penelitian mengikuti grafik distribusi normal atau tidak[4]. Data yang berdistribusi normal akan menunjukkan data
yang simetris dan
berbentuk seperti lonceng.
Uji normalitas penting untuk dilakukan
karena digunakan sebagai syarat dalam banyak metode statistik dan pengujian, salah satunya adalah dengan uji
t. Ketika
data yang didapatkan mengikuti
distribusi normal maka dapat
dilakukan
uji t,
namun jika data tidak memenuhi syarat berdistribusi normal maka dilakukan dengan
alternatif lain seperti uji mann whitney ataupun wilcoxon. Beberapa metode yang dapat digunakan dalam
uji normalitas sebagai
berikut
:
a.
Uji
Kolmogorov-Smirnov
b.
Uji
Shapiro-Wilk
4.
Uji Homogenitas
Uji homogenitas merupakan salah satu prosedur statistik dengan tujuan
melakukan pengujian apakah kelompok-kelompok sampel yang akan diuji
memiliki varians yang
berbeda secara
signifikan atau justru
sebaliknya sebaliknya. Atau
dengan kata lain uji
homogenitas memiliki tujuan untuk mengetahui dan memastikan memastikan bahwa kelompok-kelompok
sampel yang akan diuji memiliki varians
data yang
relatif sama. Uji
homogenitas merupakan syarat asumsi
penting dalam banyak analisis statistik diantaranya pada uji t.
Uji homogenitas yang sering dijadikan
alternatif yaitu:
a. Uji
Levene
b. Uji
Bartlet
C.
HIPOTESIS
Pengujian dengan uji t dilakukan
dengan menentukan hipotesis penelitian sebagai berikut
1. (H0) : Tidak terdapat perbedaan signifikan
antara kedua kelompok sampel.
2. (H1) : Terdapat perbedaan signifikan
antara kedua kelompok sampel.
Adapun
untuk menarik kesimpulan berdasarkan pengujian dengan membandingkan t hitung
dengan t tabel dapat dilakukan dengan kriteria sebagai berikut
1. Apabila t hitung < t tabel maka berarti hipotesis nol
(H0) diterima atau tidak terdapat perbedaan
signifikan antara kedua sampel.
2. Apabila t hitung > t tabel berarti hipotesis nol (H0) diabaikan atau terdapat perbedaan signifikan antara kedua sampel.
Selain
itu, jika pengujian dilakukan dengan menggunakan nilai taraf signifikansi atau nilai
p-value maka kriteria penarikan kesimpulannya adalah
1. Apabila p-value < 0,05 maka berarti hipotesis nol
(H0) diabaikan atau terdapat perbedaan
signifikan antara kedua sampel.
2. Apabila p-value > 0,05 maka berarti hipotesis nol (H0) diterima atau tidak terdapat perbedaan signifikan antara kedua sampel.
D.
JENIS
ANALISIS
a.
Independent
sample t test
Uji t sampel independen
digunakan untuk mengkomparasikan
rerata
dari dua kelompok sampel yang tidak saling terikat atau berkaitan[5]. Terdapat
beberapa asumsi dalam independent sample t test
·
Kelompok yang diuji tidak terikat satu
sama lain (independen).
·
Satu sampel hanya dapat muncul satu kali
dalam satu kelompok.
·
Kedua kelompok harus homogen.
t
hitung dalam independent sample t test dapat diselesaikan dengan persamaan
berikut
b.
Paired
sample t test
Uji t sampel berpasangan diaplikasikan guna membandingkan rerata dua kelompok sampel yang saling
terkait atau berpasangan. Syarat utama dalam pengujian ini adalah adanya dua
kelompok sampel yang saling berpasangan dan data terdistribusi normal serta
homogen. Persamaan untuk menentukan t hitung dalam paired sample t test seperti berikut ini :
c.
Single
sample t test
Single sample t test
diaplikasikan
guna
membandingkan rerata
nilai suatu sampel dengan rerata
nilai kelompok yang lebih besar (populasi). Nilai t hitung ditentukan dengan
persamaan sebagai berikut :
BAB II
CONTOH KASUS PRAKTIK STATISTIK UJI T
A.
CONTOH
KASUS YANG SESUAI
1.
Penelitian
Chairatul Umamah dkk pada tahun 2021 yang bertujuan mengeksplorasi pengaruh model inkuiri terbimbing
berbantuan alat peraga terhadap pemahaman konsep peserta didik[6].
Penelitian tersebut dalam proses analisis data yang didapatkannya
menggunakan analisis independent sample t-test. Penelitian menggunakan dua
kelompok sampel yang tidak saling berhubungan antara kelas eksperimen dan kelas
kontrol. Analisis diawali dengan melakukan pengujian prasyarat analisis dan
didapatkan hasil bahwa uji Shapiro-wilk menunjukkan data kelas kontrol dan
kelas eksperimen mempunyai
nilai signifikansi
> 0,05 yang memberikan
arti bahwa kedua data tersebut terdistribusi normal. Uji selanjutnya
adalah dilakukan uji independent sample t-test dengan bantuan IBM SPSS 25 dan
didapatkan nilai signifikansi sama dengan 0,000. Hasil yang diperoleh ini dapat
diambil keputusan bahwa H0 ditolak dan Ha diterima yang
artinya terdapat perbedaan signifikan antara kelas eksperimen dan kelas kontrol
dalam penelitian.
2.
Data
penelitian skripsi yang bertujuan mengetahui perbedaan pemahaman konsep siswa
antara sebelum dengan
setelah
penggunaan modul elektronik dengan pendekatan STEAM berbasis web.
|
No |
Pretest |
Posttest |
|
1 |
30 |
78 |
|
2 |
33 |
83 |
|
3 |
25 |
95 |
|
4 |
45 |
70 |
|
5 |
30 |
80 |
|
6 |
48 |
80 |
|
7 |
33 |
90 |
|
8 |
53 |
85 |
|
9 |
55 |
88 |
|
10 |
28 |
90 |
|
11 |
33 |
73 |
|
12 |
18 |
80 |
|
13 |
18 |
90 |
|
14 |
48 |
90 |
|
15 |
33 |
88 |
|
16 |
30 |
78 |
|
17 |
30 |
78 |
|
18 |
35 |
80 |
|
19 |
30 |
75 |
|
20 |
38 |
85 |
|
21 |
50 |
70 |
|
22 |
33 |
83 |
|
23 |
35 |
80 |
|
24 |
15 |
73 |
|
25 |
30 |
73 |
|
26 |
40 |
88 |
|
27 |
30 |
90 |
|
28 |
30 |
83 |
|
29 |
18 |
80 |
|
30 |
45 |
70 |
Hasil
Uji Normalitas dan Homogenitas
Berdasarkan hasil uji
normalitas Saphiro-Wilk yang telah
dilakukan
diketahui bahwa kedua data pretest dan posttest berdistribusi normal dan berdasarkan hasil uji homogenitas Levene-Statistics menunjukkan bahwa data
bersifat homogen. Sehingga pengujian selanjutnya dapat menerapkan analisis statistik parametrik uji t berpasangan.
Hipotesis
penelitian :
·
H0 = Tidak terdapat perbedaan
pemahaman konsep siswa antara sebelum dan sesudah penggunaan modul.
·
H1 = Terdapat perbedaan
pemahaman konsep siswa antara sebelum dan sesudah penggunaan modul.
B.
PRAKTIK
STATISTIK SECARA MANUAL TERHADAP KASUS
1.
Membuat
hipotesis penelitian
2. Membuat hipotesis statistik
3. Membuat taraf signifikansi
4.
Pedoman
penarikan kesimpulan
·
Jika nilai t hitung > t tabel maka H0
ditolak.
· Jika
nilai t hitung ![]() t tabel maka H0
diterima.
t tabel maka H0
diterima.
5.
Menghitung
nilai t hitung dan t tabel
a.
Tabel
bantuan
|
No |
Pre(X1) |
Post(Y1) |
D |
D2 |
|
1 |
30 |
78 |
48 |
2304 |
|
2 |
33 |
83 |
50 |
2500 |
|
3 |
25 |
95 |
70 |
4900 |
|
4 |
45 |
70 |
25 |
625 |
|
5 |
30 |
80 |
50 |
2500 |
|
6 |
48 |
80 |
32 |
1024 |
|
7 |
33 |
90 |
57 |
3249 |
|
8 |
53 |
85 |
32 |
1024 |
|
9 |
55 |
88 |
33 |
1089 |
|
10 |
28 |
90 |
62 |
3844 |
|
11 |
33 |
73 |
40 |
1600 |
|
12 |
18 |
80 |
62 |
3844 |
|
13 |
18 |
90 |
72 |
5184 |
|
14 |
48 |
90 |
42 |
1764 |
|
15 |
33 |
88 |
55 |
3025 |
|
16 |
30 |
78 |
48 |
2304 |
|
17 |
30 |
78 |
48 |
2304 |
|
18 |
35 |
80 |
45 |
2025 |
|
19 |
30 |
75 |
45 |
2025 |
|
20 |
38 |
85 |
47 |
2209 |
|
21 |
50 |
70 |
20 |
400 |
|
22 |
33 |
83 |
50 |
2500 |
|
23 |
35 |
80 |
45 |
2025 |
|
24 |
15 |
73 |
58 |
3364 |
|
25 |
30 |
73 |
43 |
1849 |
|
26 |
40 |
88 |
48 |
2304 |
|
27 |
30 |
90 |
60 |
3600 |
|
28 |
30 |
83 |
53 |
2809 |
|
29 |
18 |
80 |
62 |
3844 |
|
30 |
45 |
70 |
25 |
625 |
|
Jml |
1019 |
2446 |
1427 |
72663 |
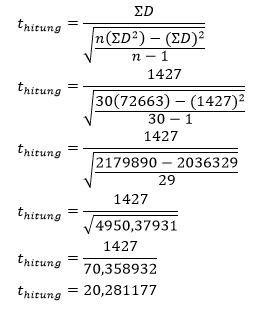
b. Substitusi persamaan t hitung
c. Menarik kesimpulan
t hitung > t tabel maka H0 ditolak
yang artinya terdapat perbedaan pemahaman konsep siswa antara sebelum dan
sesudah penggunaan modul.
C.
PRAKTIK
STATISTIK SECARA EXCEL TERHADAP KASUS
a.
Membuat
hipotesis penelitian
b.
Menentukan
kriteria pengujian
·
P
value < 0,05 maka H0 ditolak.
·
P
value > 0,05 maka H0 diterima.
c.
Menguji
statistik
·
Input data yang akan dianalisis pada
program excel
·
Klik “Data” lalu klik “Data analysis”
kemudian muncul tampilan sebagai berikut
·
Pilih t-test paired two sample means,
kemudian muncul tampilan sebagai berikut
·
Masukkan variabel range, kemudian klik OK
sehingga muncul hasil analisis.
d.
Menarik
Kesimpulan
Nilai p value = 0,00000000000000000112
atau p value <
0,05 maka H0 ditolak yang
artinya terdapat perbedaan pemahaman konsep siswa antara sebelum dan sesudah
penggunaan modul.
D.
PRAKTIK
STATISTIK SECARA SPSS TERHADAP KASUS
a.
Membuat
hipotesis penelitian
b.
Menentukan
kriteria pengujian
·
P
value < 0,05 maka H0 ditolak yang artinya terdapat perbedaan
pemahaman konsep siswa antara sebelum dan sesudah penggunaan modul.
·
P
value > 0,05 maka H0 diterima yang artinya tidak
terdapat perbedaan pemahaman konsep siswa antara sebelum dan sesudah penggunaan
modul.
c.
Menguji
statistik
·
Input data pretest dan posttest pada
spss
·
Klik “Analize” kemudian pilih “Compare
Means” dan “Paired sample t test” sehingga muncul tampilan berikut
·
Masukkan masing-masing variabel kemudian
klik OK sehingga muncul
d.
Menarik
Kesimpulan
Nilai p value = 0,000 atau p
value < 0,005 sehingga p-value
< 0,05 maka H0 tidak diterima dan berarti terdapat perbedaan
pemahaman konsep siswa antara sebelum dan sesudah penggunaan modul.
BAB III
PENUTUP
A. KESIMPULAN
Uji
t adalah salah satu metode yang
digunakan dalam proses analisis data melalui perbandingan
nilai rata-rata dari dua kelompok sampel penelitian. Analisis data dengan uji t
harus memenuhi beberapa syarat dan asumsi diantaranya adalah jumlah sampel,
jenis data, uji normalitas, dan uji homogenitas. Terdapat tiga jenis uji t
yaitu paired sample t-test, independent
sample t-test, dan single sample t-test.
Pengujian dengan uji t dapat dilakukand dengan menggunakan metode manual,
berbantuan excel, dan berbantuan SPSS.
B. SARAN
Saran
bagi pembaca sebaiknya memperbanyak sumber bacaan lain untuk memperkuat
pemahaman mengenai uji t.
DAFTAR
RUJUKAN
[1] D.
Sugiyono, “Metode penelitian pendidikan pendekatan kuantitatif, kualitatif dan
R&D,” 2013.
[2] D. George dan P. Mallery, IBM SPSS
statistics 26 step by step: A simple guide and reference. Routledge, 2019.
[3] N. Leech, K. Barrett, dan G. A. Morgan, SPSS
for intermediate statistics: Use and interpretation. Routledge, 2013.
[4] R. Ananda dan M. Fadhli, “Statistik
pendidikan: teori dan praktik dalam pendidikan,” 2018.
[5] Y. N. Hanief dan W. Himawanto, Statistik
pendidikan. Deepublish, 2017.
[6] C. Umamah, H. J. Andi, dan S. Aisah,
“Pengaruh Model Inkuiri Terbimbing dengan Alat Peraga Barbeku terhadap
Pemahaman Konsep Siswa pada Materi Hukum Newton,” J. Pendidik. MIPA,
vol. 11, no. 2, hlm. 142–150, 2021.
.png)













.png)
Komentar
Posting Komentar